Last year, Tim Bray ran a mini-investigation, based on the idea of parallelising traditionally linear tasks. He wrote a simple web logfile analyser, without any fancy tricks, and watched other people beat its performance in various ways, providing colour commentary along the way. (Should that be color commentary, given that we don't actually have that phrase in British English?). He called it Wide Finder, and the results, although somewhat unscientific because of the constraints he was under, showed the best performance in terms of elapsed time on a multicore T5120 some three orders of magnitude better than Tim's linear implementation in Ruby, with about an order of magnitude more code. The T5120, as Tim pointed out, is the shape of the future, both in the data centre and on the desktop; it doesn't matter who your processor designer of choice is, these things are in scale out rather than scale up mode for at least the next few years.
Now, he wants to do it again, only better: Wide Finder 2 gives people the opportunity to write their own faster version of Tim's linear code in whatever way they want, and to run it on a T2000. Tim is concerned with a balance of complexity and performance; complexity is mainly being measured in LOC, which is probably reasonable to get things going. The crucial idea is that we need techniques for taking advantage of modern multi-core and multi-thread techniques in processors that don't require everyone to be experts in concurrency and multiprocessing. This could prove interesting.
There are three things that I think we should try to shed some light on after WF-1. If you look back over the results, several use memory mapping to reduce the I/O overhead as much as possible, and then have multiple workers go over the space of the file, in chunks, either with OS threads or processes as workers, or something managed by the VM of the language itself. Either you have lots of little chunks, or you have as many chunks as workers, which I'd guess is less strain on the data pre-fetch scheduler in the operating system. Whatever, we're talking about data decomposition with independent data (as in: the processing of each individual log line is independent of other log lines or the results of their processing). This is the easiest kind of data decomposition. So: three things we can investigate from here.
- Can we do data decomposition in the independent data case automatically?
- For the kinds of problems that we know data decomposition with independent data works well, can we come up with better approaches?
- Are there reasonable kinds of problems for which data decomposition is either much too complicated or simply not applicable?
I'll tackle my thoughts on each of them separately, in that order. Most of the stuff I've done is on the first one, as this seems the most interesting to me.
Can we do data decomposition in the independent data case automatically?
There are two ways I can think of for doing this, one of which isn't strictly automatic but is more applicable. This is assuming that all your data comes from the same place to start off with, and that everything's running on one machine, although I'm pretty sure both of those could be lifted with a bit of cleverness (the setup becomes harder, but the user code should remain the same).
Cheating
The first way is kind of cheating. Assume we're dealing with a single loop over the data in the linear case, ie a single reduction. If you write your loop using a line iterator or generator, you can put it all in a function which takes a line generator and some sort of accumulator; a library can then drive your function and take care of making it work in parallel. Let's work through an example in Python to see how this might work. I'm not going to do the WF-2 example like this yet, because it's close to 100 lines long. Let's just calculate the arithmetic mean of a list of integers. This is pretty easy to do in the linear style.
import sys
f = open(sys.argv[1])
n = 0; s = 0
for line in f.readlines():
try:
i = int(line)
s += i
n += 1
except:
# ignore invalid lines
pass
print (float(s) / n)
So we change things around so we're not driving the loop any more.
import sys, parallel
def processor(lines, driver):
acc = driver.get_accumulator()
for line in lines:
try:
i = int(line)
acc.acc('s', i)
acc.acc('n', 1)
except:
pass
return acc
result = parallel.process(sys.argv[1], processor)
print (float(result['s']) / result['n'])
This is very similar in terms of both plain LOC and complexity, although of course there's stuff hiding in the parallel module. For a linear implementation, that's another 50 odd lines of code; for a fairly simple parallel implementation using mmap and a pipe-fork approach, it's over 100. It's tedious code, and not as efficient as it could be; my aim isn't to build this for real, but to nudge towards an existence proof (really an existence hunch, I guess). I won't bother showing it here for that reason, and because the point is that it's infrastructure: it gets written it once so the user code doesn't have to worry about it. Mine is basically Sean O'Rourke's WF-1 winner, translated to Python.
Forking a load of children costs time, moving partial results around and accumulating them takes time, and that can overwhelm the advantages of running on multiple cores when you don't have a large data set; for the simple arithmetic mean, you have to have larger files than I could be bothered with to show an improvement; doing a similar job of counting Unix mbox From_ lines, the parallel version across eight cores was about three times better than the linear version. I haven't bothered trying to optimise at all, so it's likely I'm doing something dumb somewhere.
import sys, parallel
def processor(lines, driver):
acc = driver.get_accumulator()
for line in lines:
try:
if line[0:5]=='From ':
acc.acc('n', 1)
except:
pass
return acc
result = parallel.process(sys.argv[1], processor)
print result['n']
Some empirical data, for the Unix mbox job: running on a machine with dual quad-core 1.6GHz Xeons, averaging over 10 consecutive runs from warm (so the roughly 1GB file should already have been in memory somewhere), we get the following. (Note that the GNU grep(1) does it in a little more than two seconds; this is always going to be a toy example, so don't read too much into it.)
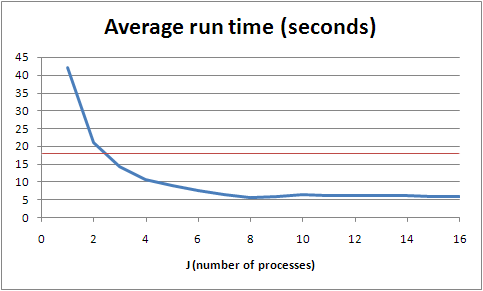
The red line is the mark for my naive linear implementation; its main advantage is that a lot of the work is being done in the interpreter, in C, rather than in my code, in Python. This makes a big difference - the parallel version seems to be doing about 2.5 times as much work. It's worth noting that this machine is not completely unloaded; it's multi-user and also acts as a web and mail server, amongst other things, so beyond J=6 we're seeing slightly more flaky numbers. Back-of-the-envelope monitoring, however suggests that we don't start getting interference from other processes on the box before we start seeing interference from its own processes, where J=9 and we run out of cores (although the system does a reasonably good job of keeping things going from there up).
Note that there's some interesting discussion going on around WF-2 about how to scale some of these techniques up to gigabytes of input in one go; Alex Morega in particular has been using a broadly similar approach in Python and hit some interesting snags, and I urge you to read his write-up for details. Either we'll come up with new idioms that don't have these problems, or we'll improve the things we depend on (languages, libraries, VMs, operating systems...) to allow us to work better at scale without radically changing the way we code. (I'm sure there are some great approaches to these problems that I haven't heard of - with luck, WF-2 will bring them to a wider group of people.)
Enough on this. Hopefully I've convinced you that this is entirely feasible; it's a matter of someone writing a good library to drive it all.
Not cheating
In order to be more automatic, we need to convert the original linear style into the parallel style entirely programmatically. To my knowledge, you can't do this in Python. In fact, many languages, even dynamic languages, don't want you dicking around directly with live code constructs, which limits the applicability of this idea somewhat. However it's entirely possible to imagine that we could, in some theoretical super-Python, write the following and have the parallel module rewrite the process function appropriately.
import sys, parallel
def process(file):
f = open(sys.argv[1])
result = { 'n': 0, 's': 0 }
for line in f.readlines():
try:
i = int(line)
result['s'] += i
result['n'] += 1
except:
pass
f.close()
print (float(result['s']) / result['n'])
parallel.apply(process, sys.argv[1])
In complexity for the programmer, this is like a halfway house between the linear and parallel approaches above, with the nice advantage that it doesn't remotely look parallel except for the last line.
I'm certain it is possible because the only things that enter the loop either can be considered immutable (in the scope of the loop), or are the file object f (which we only ever apply readlines() to), and the only thing that escapes the loop is a dictionary, and that within the loop we only ever accumulate into that dictionary. It's not beyond the bounds of programming ability to spot this situation, and convert it into the cheating version above. Although it's probably beyond my programming ability, and certainly is in Python. In fact, we could probably write a parallel.invoke() or something which is given a Python module, and parallelises that, at which point we've got a (limited) automatic parallel Python interpreter. Again, providing you can mutate Python code on the fly.
A question which arises, then, is this: given the constraints of only being able to parallelise loops over quanta of data (for instance, iterating over log lines, or 32 bit words, in a file), with immutable inputs and a number of dictionary outputs, how large is the problem space we can solve? This is actually question three on the original list, so I'll leave it for now.
Another is whether we can lift any of these restrictions, the main one being accumulation. (And I'm counting subtraction as accumulation, for these purposes.) Assuming data independence, there aren't actually many alternatives to accumulation: I can only think of multiplication, which is the same as accumulation anyway, give or take some logarithms. So I'm guessing the answer to this question is an unwelcome "no"; however I'm probably wrong about that. You can do an awful lot with accumulation, though.
For the kinds of problems that we know data decomposition with independent data works well, can we come up with better approaches?
I'll be very disappointed if the answer to this isn't "yes". However I don't think WF-2 is necessarily going to show us much here by being almost tuned to this kind of approach. I'm probably wrong about this as well, though, and new ways of thinking about these kinds of problem would be great.
It's not clear to me, because I don't understand the languages well enough, whether all the techniques that were used in WF-1 with JoCaml and Erlang are covered by data decomposition (beyond things like optimising the matcher). Even if there aren't, there are undoubtedly lessons to be learned from how you structure your code in those languages to approach these problems. This partly falls under the previous question: if we can't automatically parallelise our old ways of doing things, then we want new idioms where we can.
Are there reasonable kinds of problems for which data decomposition is either much too complicated or simply not applicable?
The simple answer is "yes", but that's in general. WF-2 is concerned with what most programmers will have to deal with. Here, I wonder if the answer might be "no". You can do an awful lot without sacrificing data independence. I calculated the arithmetic mean earlier, but for instance you can do standard deviation as well, providing you defer most of the computation until the end, and are prepared to unwind the formula. Generally speaking, we don't seem to actually do much computation in computing, at least these days. I think this means that for most people, beyond this one technique, you don't have to worry about parallelism too much at the moment, because anything that isn't linear to start off with (like, say, web serving) is already scaling pretty well on modern processors. So if we can use data decomposition automatically in some common cases, we dodge the bullet and keep up with Moore's Law for a few more years.
Dependent data decomposition
Data decomposition continues to be useful even with related data; however you start getting into I/O or memory model issues if your data set starts off all jumbled up, as it is in WF-2, because you've got to sort it all to get it into the right worker. For instance, if you want to do logfile analysis and care about sessions, it becomes difficult to do anything without arranging for all the data within a session to go to the same worker. (Not impossible, but in the context of making it easy on programmers, I think we can ignore that case.) In most cases, you're better off filtering your data once into the right buckets, ideally at the point you collect it; you can of course parallelise filtering, but if you're doing that at the same time as your final processing, you're moving lots of data around. The only situation I can think of where it's not going to help to filter in advance is if you need to do different processing runs over the data and your dependencies in the processing runs are different, resulting in a different data decomposition. On the other hand, I can't think of a good example for this. I'm sure they exist, but I'm less sure that they appear to regular programmers.
Note that in my parallel module above, for dealing with an independent data problem, I made a silent assumption that it's cheaper to not move much data around between the parts of your system; so it's far better for the controlling part of the system to tell a worker to attack a given byte range than it is to actually give it that data. This is surely not true in the general case, which is great news for dependent data decomposition. Given suitable VM infrastructure, or an appropriate memory model, this shouldn't actually be a problem; it's just that for most languages on most platforms at the moment, it seems to be. On the other hand, once you scale beyond a single machine, you really want the data you're working on to be close to the processing; a large part of the magic of Hadoop seems to be about this, although I haven't looked closely.
First results for WF-2
First results for WF-2 are beginning to come in. Ray Waldin set the bar using Scala, taking Tim's thousands of minutes down to tens. By now the leaders are running in minutes - note that if the ZFS pool can pull data at 150Mbps, as the Bonnie run showed with a 100G test, then the fastest all the data can come off disk is a little under five minutes; we're seeing results close to that already.
I'll start posting timings from my runs once I get it up to the complete data set; I'm also looking at how the use efficiency changes by number of workers across the size of input file, since Tim has conveniently provided various sizes of live data. So this might take a few days; and there's a chance my times will be embarrassingly bad, meaning I might just not publish :-)
A final point
There's a great book called Patterns For Parallel Programming, by Mattson, Sanders and Massingill (if you're not in Europe you may prefer to get it from Amazon.com). It has a lot more detail and useful thoughts on parallelism than I could ever come up with: although I have some experience with scaling and data processing, these guys do it all the time.