How to construct Penrose tilings

This information is widely available on the web, but for some reason no page seems to give the two well-known kinds of Penrose tiling the same treatment in a consistent way – every page I've seen concentrates on one of the two tilings and mentions the other only in passing. So here are my own notes.

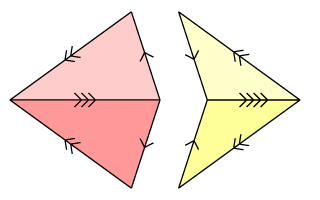
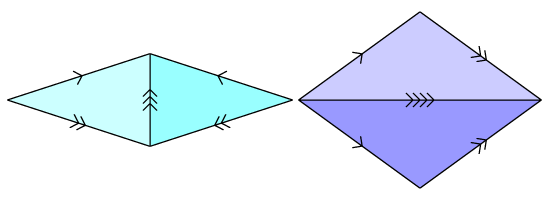
The two well-known types of Penrose tiling are the one with darts and kites (called ‘P2’, I think simply because it was the second one Penrose discovered after the boring one with six types of silly tile) and the one with two shapes of rhombus (called ‘P3’).

For both tilings, we must divide the tiles in half to get triangles. I mark all the edges of the triangles to indicate how they can fit together: the three- and four-arrow edges force the triangles to join into their appropriate full Penrose tiles, and the one- and two-arrow edges force the Penrose tiles to fit together in ways that are aperiodic. Note that in each type of tiling, each of the two triangles appears in both of its mirror-image forms (leading to eight triangle types in total, if you really want to look at it that way).

(Note that for the two types of tiling, the sizes of the triangles have to match up differently: for P2 the acute triangle's legs are the same length as the obtuse one's base, whereas for P3 the legs of both triangles are equal in length.)

Now all we need is the rules for splitting up each of those four types of triangle during deflation:

You should be able to verify that the two diagrams for each tiling have the correct consistency properties:

• the one-arrow and two-arrow edges translate into the same pattern of arrows no matter which type of triangle they appear on:
  • in P2, > always becomes >>, and >> always becomes << >>>>
  • in P3, > always becomes << <<<, and >> always becomes <<<<
• in the subdivided versions of both types of triangle, all the two-arrow lines are the same length (namely $\phi$ times the length of the two-arrow lines in the original triangles).

Those consistency properties guarantee that iterating the expansion process a fixed number of times starting with any one triangle must give an arbitrarily large chunk of tiling with all triangles matching up in the ways required by the arrows – which we can demonstrate by cranking up the recursion depth in the Postscript that generated the above diagrams:

Note also that this construction all by itself can be used to show the non-periodicity of the generated tiling. For both types of tiling, we can identify a type A and type B triangle such that the subdivision rules map an A into two As and one B, and map a B into one A and one B. (For P2, A is the acute triangle; for P3, A is the obtuse one.) So if you have an ordered pair $(a,b)$ denoting $a$ triangles of type A and $b$ of type B, then subdividing all triangles once maps $(a,b)$ to $(2a+b,a+b)$, and an easy induction shows that iterating that transformation $n$ times must map $(a,b)$ to $(F_{2n+1}a+F_{2n}b,F_{2n}a+F_{2n-1}b)$. So the ratio between the two types of triangle approaches $\phi$ with increasing subdivision, and hence we cannot be looking at a subdivision of any periodic tiling (because the ratio would instead have to approach the necessarily rational ratio in the repeated segment).

I can't immediately see how to prove that you can inflate any valid tiling into a larger one by reversing the subdivision rules. It's probably tedious case analysis about what combinations of triangles can possibly surround any given one. But from a proof of that would follow the impossibility of any periodic tiling with these tiles (having shown that tilings generated by subdivision have the two triangle types in golden ratio and hence are nonperiodic, we complete the proof that all tilings are nonperiodic by showing that all tilings can be generated by subdivision), and also Conway's theorem about always being able to find a duplicate of any finite piece of tiling.