Different people have different conventions for how to rank the Olympic medal results. Some people prefer to count total medals first, and only look at the individual number of gold, silver and bronze medals in order to break ties. Some people, on the other hand, prefer to count gold medals first, break ties using silver medals, and break any persisting ties using bronze. In between those two extremes, there are any number of other reasonable rankings: for instance, one could adopt a points system allocating three points for a gold medal, two for a silver and one for a bronze. (Better still, if you allocated π2 for a gold, π for a silver and 1 for a bronze, there could never be any tie in the total scores except when two countries had exactly the same medal counts in all three categories!) Any of these ranking systems, or quite a few others, could reasonably be argued to be some sort of measurement of how successful (in absolute terms) a country had been at winning medals; but each would place the 87 medal-winning countries in a different overall order.
With all that scope for reasonable disagreement, is there anything we can all agree on? How much of the hierarchy in the medal table is indisputable, and how much depends on your point of view?
(I'll restrict the following discussion to the absolute ranking of countries, solely by their medal counts. There is a lot of scope for reasonable comparisons which try to offset countries' natural advantages due to size or wealth, or which are more interested in some kinds of sport than others, but that's outside the scope of what I'm discussing here.)
There are two basic constraints which are common to all the above possibilities, and which must be obeyed by any "reasonable" absolute ranking system:
So we want to say that one country has done strictly better than another if the medal score of the latter can be transformed into the former by a sequence of medal additions and medal upgrades. A bit of thought shows that this is exactly equivalent to defining a partial order on triples of medals, in which a triple (G,S,B) is considered at least as good as another triple (g,s,b) if and only if it satisfies the three conditions
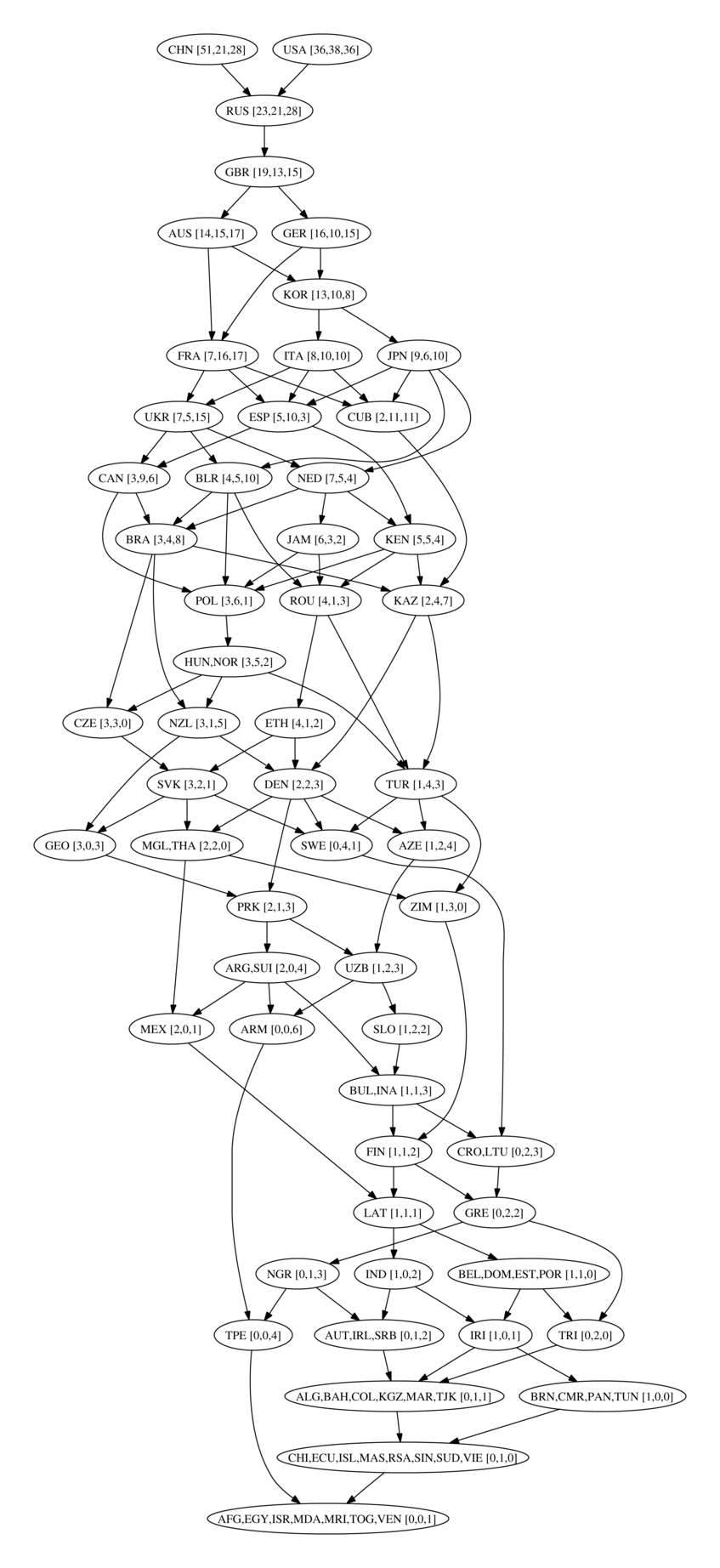
Based on this criterion, we can analyse the results of an Olympic Games to determine all the unarguable relationships within the medal ranking table, and distinguish them from those which are matters of opinion. Here I present the results of applying this procedure to the Beijing 2008 Olympics results. The diagram below is a Hasse diagram: a country has unarguably done better than another country if there is a chain of arrows running from the former to the latter. If two countries are not connected by a chain of arrows in either direction, it means that there is scope for legitimate dispute about which has done better.

(Transitive reduction and graph drawing courtesy of the rather nifty Graphviz.)